krotboards.blogg.se

1. #STANDARD DEVIATION IN EXCEL GRAPH FROM DATA SET HOW TO#
2. #STANDARD DEVIATION IN EXCEL GRAPH FROM DATA SET FULL#

Looking across the three age groups, we observe that consumers aged between 30 and 45 spend on average more than the two other groups (mean and median). The data is likely to be skewed to the right since the median is slightly lower than the mean value. This means that half of the respondents spend more than 139 USD and the other half less than 139 USD. The mean shows that respondents globally spend 156 USD on average per month in online shopping. standard deviation, range, variance, variation coefficient), that describe data variability.ĭefinitions and formulas can be found in the XLSTAT Help menu (click on Help button in the dialog box). mean, median) that give information around the center of the data, and the measures of dispersion (e.g. The most commonly used basic statistics are the measures of the central tendency (e.g.

#STANDARD DEVIATION IN EXCEL GRAPH FROM DATA SET FULL#

A full set of descriptive statistics is displayed for all respondents (column B) as well as per age class (columns C-E). The results are displayed on the new sheet named Desc. Interpreting descriptive statistics for quantitative data In the Outputs tab, click the **All button to select all the statistics for quantitative data. That is more interesting in the case of several variables measured on different scales.ĥ. Since we are only dealing with one single variable we do not choose the Normalize or Rescale** option. In this tutorial, we focus on descriptive statistics so we do not activate Charts. In the Options tab, activate the following options: These include the variable name as a prefix and the category name as a suffix.įinally, select the Sheet option in order to display the results on a new sheet and the Sample labels to consider the first row of the data table as labels.Ĥ. We also want to display Variable-Category labels in the output. Then select the column corresponding to the age class in the Subsamples field. In the General tab, select the column corresponding to the money spend on online shopping in the Quantitative data field. The Descriptive Statistics dialog box appears.ģ. Once XLSTAT is open, select the XLSTAT / Describing data / Descriptive statistics command as shown below.Ģ. Setting up the dialog box for descriptive statisticsġ. This will allow us to extract important information from the survey and detect potential differences between the groups.

The standard deviation, the variance and the variation coefficient, that reflect the dispersion. The mean and the median, that reflect the central tendencyĢ. Our goal here is to summarize the results per age group using common descriptive statistics, such as: 1. Rows correspond to respondents and columns to the amount of money spent as well as the age group they belong to. The data represent the results of a survey on the amount of money people spend in online shopping on a monthly average basis.

#STANDARD DEVIATION IN EXCEL GRAPH FROM DATA SET HOW TO#

Example of the situation when we want data to have large standard deviation is the quality score of the rival's product.This tutorial shows how to compute and interpret the mean, the median, the standard deviation and other descriptive statistics for quantitative data in Excel using the XLSTAT software. What is an example of when you would want consistent data and therefore a small standard deviation?Įxample of the situation when we want data to be consistent, and therefore, a small standard deviation is the positive performance of a cricketer.

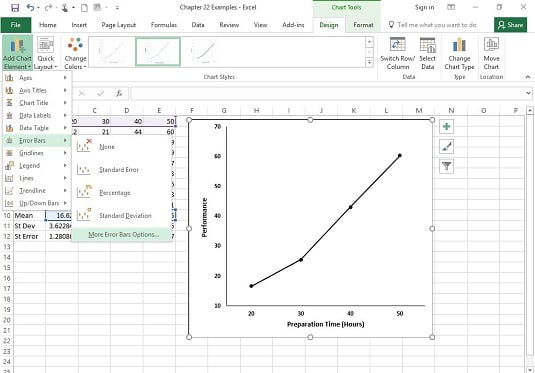
When the standard deviation is large, the curve will be short and wide in spread. When the standard deviation is small, the curve will be tall and narrow in spread. The center of the graph is the mean, and the height and width of the graph are determined by the standard deviation. How do you know if standard deviation is small or large? Which data set has largest standard deviation? As we can see, the data values from set D are the farthest from its mean out of all the data sets (four of its 5 values, -50, 33, 34, and 35, are farther from 10 than any values in the other data sets) thus, set D has the greatest standard deviation. If all points in the distribution are the same, then the mean is the same as each distribution point. A deviation is a data point's distance from the distribution mean. This occurs when each element of the distribution is the same. The smallest standard deviation possible in a distribution is 0. Keeping this in consideration, what is the smallest standard deviation? The smallest possible standard deviation for any set is 0, and the standard deviation of a set will be zero when all the data points are the same.